
Designed by Diptatanu Das
Part 1: The Thermodynamic Background
Young Monsieur Sadi Carnot, a French mechanical engineer, boldly retired from military services at 24. Because he was curious about the physics behind steam engines and wanted to improve their efficiency[i].
He quickly learned that a steam engine worked not by only consuming calories but by transferring the heat from a warm to a cold reservoir. Moreover, the engine’s efficiency was directly dependent upon the temperature difference between the reservoirs. He further realized that the machine would not work when the temperature difference was absent.
Carnot eventually published his observations and inferences in his book Reflexions sur le puissance motrice de feu in 1824. This book turned out as a milestone work in the scientific discipline of classical thermodynamics.
Although the contemporaries neglected the work during his lifetime, today, any high school student takes the topic of Carnot’s Cycle as granted. People, nowadays also rightfully regard Carnot as the father of classical thermodynamics.
Sadly, such a prodigy died too young due to cholera. As a result, many of his scientific records were burnt down and forever lost into oblivion.
But the journey of thermodynamics did not come to a halt. From 1824 to 1851, eminent scientists like Rudolf Clausius, Lord Kelvin, and Cano began to develop a theoretical framework that addressed the drawbacks of the Carnot’s Cycle[ii]. Eventually, these scientists postulated the second law of Thermodynamics that introduced us to the concept of entropy for the first time. Meanwhile, the first law of Thermodynamics was proposed around 1840 by Rudolf Clausius.
See more about Thermodynamics.
In broad terms, Thermodynamics is a discipline of study that deals with how the energy of
one form gets converted to another. It gives us the relation between variables like heat, work,
temperature, and energy that define a physical system, using the following:
PV = nRT
Cp - Cv = nR
S = k loge(W)
where the terms have usual significance.
To know the exact value of these variables, one needs to resort to the concepts of Statistical Thermodynamics.
Statistical Mechanics
But before delving directly into it, let us know how the subject came into inception.
Statistical Mechanics is a branch of science that considers the concept of probability and statistics to describe a physical phenomenon in terms of the motion of a large number of microscopic particles like atoms or molecules. It was developed around the 1870s by Ludwig Boltzmann and Clerk Maxwell. Boltzmann worked on the problems like establishing the equation of the state of gases, thermal equilibrium, etc. In 1875, Boltzmann successfully derived a relation between absolute entropy and thermodynamic probability of states (Ω) of the system of gaseous particles for the first time. Thus, he established a bridge between two discrete disciplines – classical thermodynamics and statistical mechanics. Hence, the field of statistical thermodynamics was born.

(Source: Wikipedia)
Statistical Mechanics is a branch of science that considers the concept of probability and statistics to describe a physical phenomenon in terms of the motion of a large number of microscopic particles like atoms or molecules. It was developed around the 1870s by Ludwig Boltzmann and Clerk Maxwell. Boltzmann worked on the problems like establishing the equation of the state of gases, thermal equilibrium, etc. In 1875, Boltzmann successfully derived a relation between absolute entropy and thermodynamic probability of states (Ω) of the system of gaseous particles for the first time. Thus, he established a bridge between two discrete disciplines – classical thermodynamics and statistical mechanics. Hence, the field of statistical thermodynamics was born.
Statistical thermodynamics describes a system as a collection of numerous microscopic entities called an ensemble. The energy distribution between the particles is discrete, and particles are distinguishable. Thus, statistical thermodynamics is a bridge between the two extremes – classical thermodynamics and quantum mechanics.
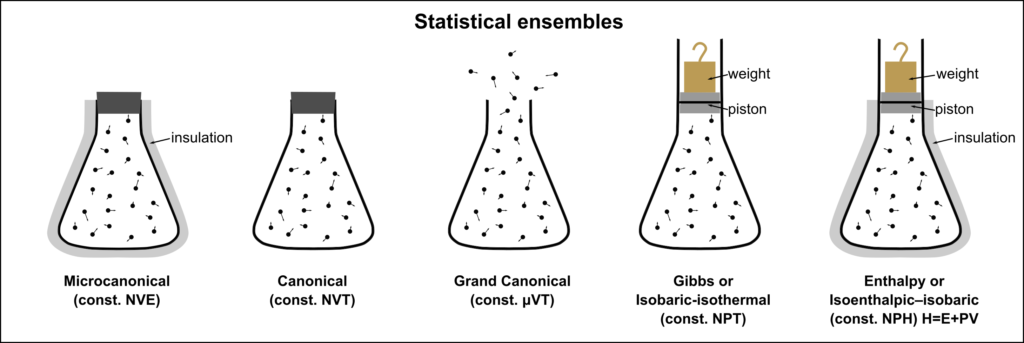
(Source: Wikipedia)
Scientists who studied statistical mechanics developed theories like partition function etc., that could relate their findings with the results already obtained from the equations from classical thermodynamics. They thought that they could explain any complex phenomenon like a phase transition, crystallization, etc. in terms of intermolecular potentials alone. But one had to solve sets of very complex analytical equations involving thousands of particles simultaneously to approach those problems. Such equations were too rigorous to be solved by mere pen and paper alone. So, an alternative way had to be used.
Luckily computers came to the rescue!
To be continued in the next part…
Author’s Bio:

Shrestha Chowdhury is currently working as a Senior Research Fellow in the Department of Chemical Sciences at IISER KOLKATA. For her third blog in TQR platform, she has attempted to pen down her thoughts on her own field of research interest such that other bright minds join the field too. She dedicates this article to a few of her beloved juniors – Mousumi Chakraborty and Diptatanu Das for their warm enthusiasm and critical review of the draft during its preparation.
References:
- Carnot discovered that a steam, the more efficient the engine Linda Hall Library
- Bo, M. “History and Realistic of the 2nd Lawof Thermodynamics” ResearchGate
2 thoughts on “Molecular Dynamics Simulation – Wizardry of Numbers”