
One of the most profound theory of all time is the General theory of relativity formulated by Einstein.
General relativity explains gravity as the curvature of space-time. It’s all about geometry. The basic equation of general relativity is called Einstein’s equation. Given in simple terms and in units where, ![]() , it transforms as shown below:
, it transforms as shown below:

This result when we consider an expanding universe. Einstein added the famous cosmological constant(λ)(not included in the above equation) as he considered the universe to be static, which was later proved to be wrong by Hubble.

the equation given by Einstein when he added cosmological constant.
Cosmological constant is the term that represents the “vacuum energy”, the possibility that empty space possesses density and pressure, thus preventing the universe from collapsing. Now let’s delve into the equation,
The equation above conceals a whole collection of equations corresponding to the possible combinations of values the μ and ν can take, The value of 0 corresponds to time and the values 1,2 and 3 to the three dimensions of space, where –![]()

And so on. For example, the following equation:
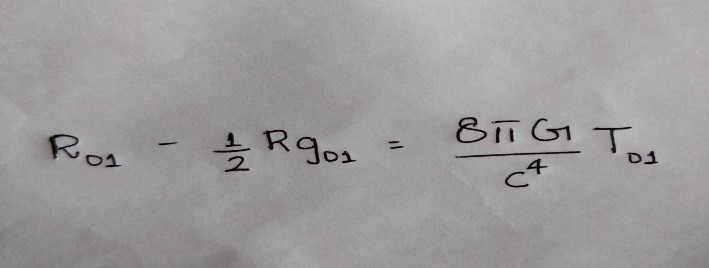
corresponds to time and the 1-direction of space. The Τ term on the right-hand side describes the momentum (speed and mass) of matter moving in the 1-direction of space. The motion causes time and the 1-direction of space to mix and warp into each other that effect is described by the left-hand side of the equation. If μ and ν both take the value 0, then the equation only relates to time. The term T(00) now stands for energy, which causes time to speed up or slow down. The left-hand side of the equation describes that change in the flow of time.
Since each of µ and ν can take on four values, this gives a total of 4 x 4 =16 equations. However, it turns out that the equation with µ=i and ν=j (for i and j each equal to one of 0, 1, 2 or 3) is the same as the equation with μ=j and ν=i. This reduces the total number of equations to ten. These 10 equations allow you to work out exactly how massive objects, such as planets, stars, galaxies, or even black holes affect the space time around them.
Now let’s see what those terms correspond to. First lets start with one of the important term “ Stress-Energy tensor” represented by T(µν) . The stress–energy tensor is the source of the Gravitational field in the Einstein field equation. The stress-energy tensor is of order two, whereas a normal vector is a 1st order tensor. The components of the stress-energy tensor include Energy density, momentum density , shear stress , pressure and momentum flux. The “G” as most of know is the gravitational constant from Newtonian gravity. The “R(µν)” is the Ricci curvature tensor and “R” is the Ricci Scalar and “g(µν)” is the metric tensor. I’ll explain the Ricci scalar and some of the necessary concepts to understand it.
Now lets assume a curved space-time as shown,

If we define an axis for one of three spatial dimensions and an axis for time, different observers moving relative to each other will have different orientations for these axes. Assume we move along time axes in direction of a small arrow. When a infinitesimally small part of this curved space is taken(assume the blue and white parts to be infinitesimally small parts) , it looks like a flat space. Now assume that the small arrow in that small flat space perpendicular to the normal of that small space(take it in any of the blue space) . If you move the arrow to the next adjacent small space , you will observer that approximation for the flat space time is no longer valid and the arrow is no longer perpendicular to the normal of that small space which means it doesn’t lie perfectly in that small plane. You have to rotate the arrow by a small amount to make it perpendicular. If you repeat the steps again ,we get the path followed through a curved space time which looks like shown below.

Keeping the above in mind, now to describe a four dimensional space we need four coordinates namely xⁱ (i=0,1,2,3) where x⁰ represents time and others represent spatial coordinates. In the case above where the red arrow moves along time axes, the gravitational acceleration is approximately equal to rate at which the basis vector(red arrow) for time changes as it move for in time and the change is due to curvature. If we repeat the process over and over again , we can displace a vector over long distances, which is known as the Parallel transport.
This is an important concept to understand. Now if we parallel transport a vector in flat space time and we return to the initial position , the vector will still point to same direction.
 assume the white space to be flat space time.
assume the white space to be flat space time.





But the same doesn’t happen in a curved space time. To illustrate this assume a Spherical space time like shown below with a red arrow(vector).
If I move the vector to north pole of the sphere(assume) and move it back to equator of the sphere but in a different position in the order shown below in the depiction,
So when I do the steps as shown above, we find that the vector no more points in the same direction but is rotated by 90⁰ . This happens as the space time is curved. You can repeat this by moving the vector to any positon in the sphere. Now how do you think it is useful to us?
This is so useful because we can define the curvature of space time in terms of how much the angle of a vector changes when it return to its original position. Note that this angle depends on that area covered when the vector travelled. As in the above pictures the vector is rotated by 90⁰ when it covered 1/8th of the area of the sphere. If we double the area the vector rotates by 180⁰(doubled)(try imagining this). Form this we can define the curvature as (amount by which vector is rotated)/(area covered by the vector when travelled).
Also note that the vector rotated clockwise when travelled in clockwise direction and same goes vice versa. So if the vector rotates in the direction it is rotated, its known as positive curvature and vice versa (try imagining and find a surface where you can have negative curvature). Now we can define the curvature at each point in curved space time in terms of R=(amount by which vector rotated)/(size of area covered) as area approaches zero for infinitesimally small parts. After all these are explained , now we are ready to understand one variable of the equation that is “R” which is the Ricci scalar. Thus I have briefly explained the “R”-Ricci scalar. I’ll explain other parts of the equation in my next blog and I’ll explain applications of General Relativity such as derivation of Gravitational waves, Schwarzschild radius and the famous mercury orbit problem. Hope you enjoyed it. Have fun learning Physics.
Please mind the mistakes as it’s my first blog.
P.S: some of the pictures don’t belong to me.
By,
ShivaSankar K A
BS-MS
IISER Bhopal.
1 thought on “Understanding a little of General Relativity”