
Maybe, the title was enough for you to guess what I’m about to discuss here. For those of you who haven’t, let’s start with a short description of it. However, before that, let’s understand the definition of natural numbers.
What are natural numbers?
Natural numbers are essentially positive integers or non-negative integers which start from 1. What I mean is that the following are natural numbers:
1, 2, 3, 4, 5, 6, 7, 8, 9,10, ……, ∞
So, time to know the real agenda!
If you are a math enthusiast, then, even if you’re quite young, there are high chances that someone has already told you that the sum of all natural numbers is exactly equal to −1/12.
Yes, you heard me right and it is, in some sense, true that 1 + 2 + 3 + … = -1/12. You may even know that this famous result has been found by none other than the great Srinivasa Ramanujan.
Sounds crazy right?
Does this make sense?
True that it is incredibly tough to make any sense of it! So, to be precise, I am here to give you an idea of why all this is true in the most non-mathematical and non-rigorous way possible. As a bonus, I will also give you a chance to win $1,000,000 at the end. So make sure you don’t take your eyes off it unless you reach the end.
However, before going into the main part, let me tell you something that one of my professors told us when we were pestering him to tell us about this equality in our analysis class. He simply said, “The summations that you see here in this theorem are not the sum that you are familiar with. This property makes sense if and only if you define summation in a different way.”
Well, I know how bizarre this statement looks to you now. But keep this in the back of your mind. Soon, things will start making sense.
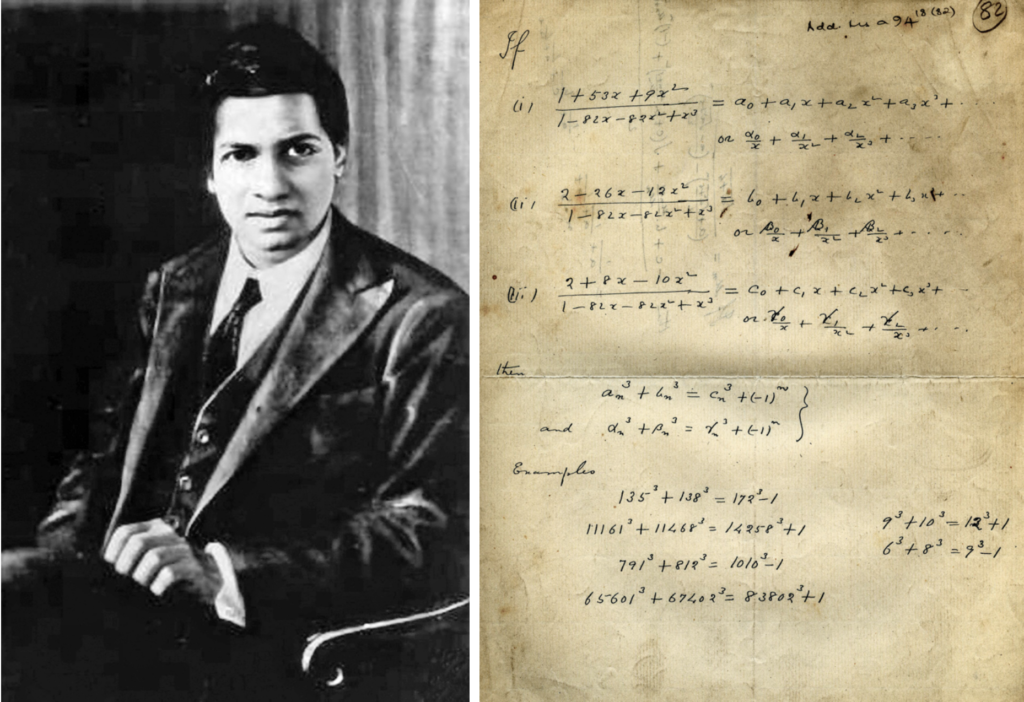
Declaration:
What’s next will require a basic understanding/concept of complex numbers and functions. If you have a basic knowledge of these, you can continue, else read the following for a minute or two first:
Sequence and Series
Be honest and admit that the name sequence speaks much for itself. A sequence in mathematics is simply a sequence of numbers.
Again, sequences need not only be of numbers in the strict sense, but in the present context, we only need numbers.
For example, here are a few sequences:
- {1,2,3,4,5,…}
- {-1,-2,-3,-4,-5,..}
- {1,0.1,0.01,0.001,0.0001,…}
- {0.9,0.99,0.999,…}
- {1,-1,1,-1,1,-1,…}
- {0.9,1.99,0.999,1.9999,0.99999,1.999999,…}
- {1,-0.1,0.01,-0.001,0.0001,…}
and so on.
Now, note that though all of these are sequences, their behaviours are quite different.
The first one goes on increasing if you go on moving to the right, and it increases on and on. Also, note that you can increase it as much as you want (i.e., if I give you any number, you can find a term in the sequence that is greater than that number). These types of sequences are said to diverge to infinity.
The second one goes on decreasing and are therefore said to diverge to minus infinity.
The third one goes on approaching 0 as you keep moving right. Also, you can make it as close to zero as you want (i.e., if I give you any positive number, you can find a term in the sequence less than that number). This sequence is said to converge to 0.
The fourth one is similar to the third and said to converge to 1.
The fifth one simply oscillates between two numbers. You cannot make it as small or as large as you want. These types of sequences are simply said to diverge.
The sixth and the seventh sequence oscillates, but still, you can make them as small as you want. So, they also converge to 1 and 0 respectively. Apart from the case of oscillatory divergent sequences, the behavior of all others can be understood in terms of convergence or divergence of light rays. Think of how these sequences would look like if you plot the points on a graph. Check out the diagrams below for a better understanding. It turns out that convergent sequences are particularly interesting to mathematicians. We have developed thousands of theories to determine whether a sequence converges or not. Of course, I can’t discuss these theories now.
Now, let’s talk about a series. Well, a series is also a sequence- it is a sequence of partial sums. A partial sum is simply the sum of terms of a series up to a particular term. In other words, the first partial sum is simply the first term of the series, the second partial sum is the sum of the first and the second term, the third partial sum is the sum of the first three terms, and so on. And the sequence that these partial sums determine is called the series with respect to the given sequences.
For example, let us consider the series with respect to the sequences mentioned above
- {1,1+2,1+2+3,1+2+3+4,…} = {1,3,6,10,15,21,…}
- {-1,-3,-6,-10,-15,-21,…}
- {1,1+0.1,1+0.1+0.01,…} = {1,1.1,1.11,1.111,…}
- {0.9,1.89,2.889,3.8889,3.88889,…}
- {1,1-1,1-1+1,1-1+1-1,1-1+1-1+1,…} = {1,0,1,0,1,0,1,…}
The next two are left as exercises for the reader. Also, try to picture how the series will look when plotted on a graph.
Note that only the third and the seventh series converge. An exercise for you is to determine the value to which they converge.
Fun exercise: Try to convince yourself (in any way you want) that if a series converges, then the corresponding sequence must converge to 0. Also, try to find an example where the converse is not true, i.e., try to find a sequence that converges to 0, but the series diverges.
Doesn’t matter if you aren’t fully convinced. We wont need this in our journey.

Sequence 1 
Sequence 2 
Sequence 3 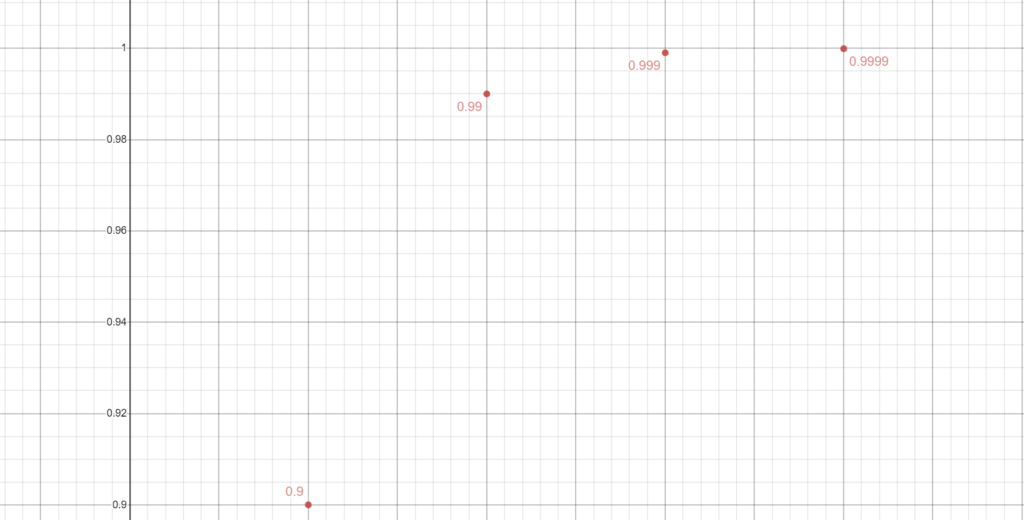
Sequence 4 
Sequence 5
A Special Sequence
So finally we arrive at the last step before reaching the heart of our matter!
One series that has been extremely notorious (no matter how innocent it looks) for mathematicians over centuries is the one corresponding to the sequence {1, 1/2, 1/3, 1/4, …}. Believe it or not, it has baffled mathematicians over two whole centuries before finally revealing to a mathematician named Pietro Mengoli (although now we know that Nicole Oresme was actually the first mathematician to prove it, that proof got lost until it was recovered much later) that it diverges.
One reason why tracking it down was so hard was that it diverges very very slowly, almost with an illusion of convergence.
So, rewriting it in mathematical terms,
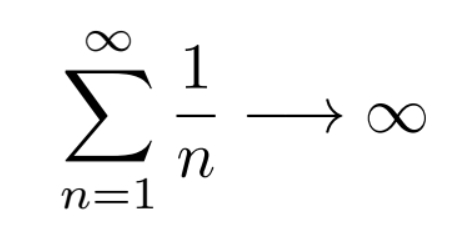
Don’t be afraid of the notations- the S-like creature on the left is a sum representing the fact that we are summing 1/n from n = 1 all the way up to infinity, and the arrow simply says that this sum goes to infinity.
However we have much more than this here. We have proved in all rigour that
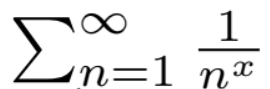
converges for all x > 1 and diverges for all x ≤ 1. That is,
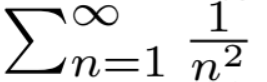
converges,
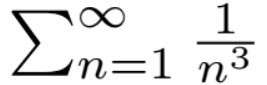
converges,
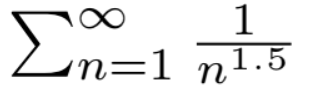
converges, but,
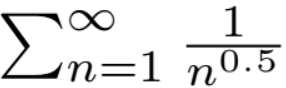
and,
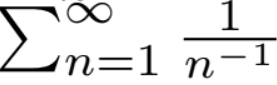
diverges.
The behaviour of these sequences takes us to the heart of the matter.
Riemann Zeta Function

So, finally, we are here. If you have made your way up to this point, maybe this is a good time to take a small break, have your coffee, and finally return to the climax.
We learnt in the previous section that the series,
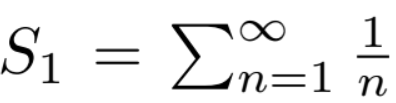
does not converge. We also learnt that,
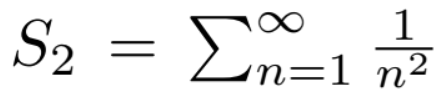
converges and so does Sx for any x > 1.
This is enough motivation for a mathematician (of such proportions as of Riemann) to define a function ζ(x) as,
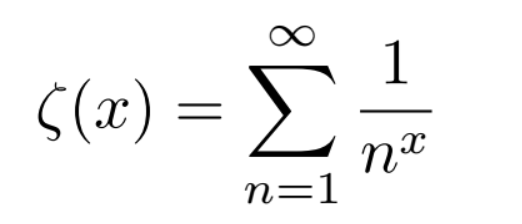
In other words,
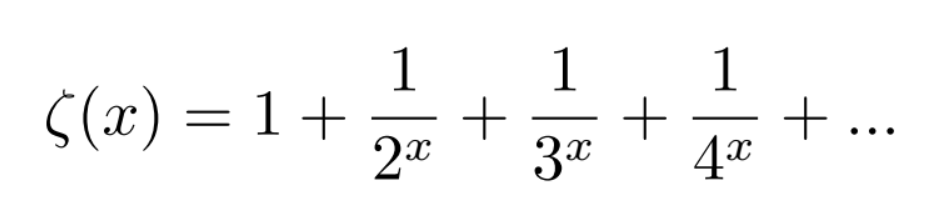
Clearly, this function is well defined only for x > 1 as the series we are dealing with gives a definite value only if x > 1. When x ≤ 1, the series in concern diverges and hence doesn’t make sense.
In case you are still a little uncomfortable with the notations, you may think of it like this- ζ(x) is a function that takes in a real number greater than 1, calculates the sum,
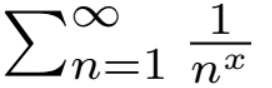
and gives you this result.
Now comes what a mathematician usually does to a topic when it becomes well understood in a smaller part of a larger set.
Now that we know how the function behaves for any real x > 1, let’s see what happens if x is a complex number. Well, it turns out (for reasons outside the scope of the present discussion) that ζ((a, b)) converges if and only if a > 1. Note that this is in absolute harmony with our previous results as the part of the plane which has points (a, b) with a > 1 contains those points (x, 0) in which x > 1, i.e., all real numbers greater than 1. So, a known result over the reals is generalized to the complex numbers.
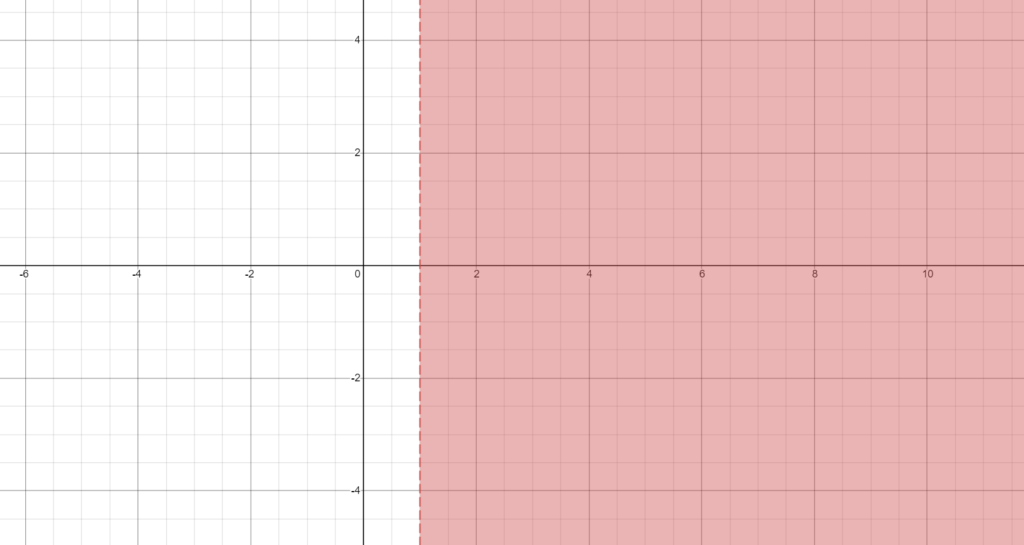
Now, before taking you through another generalization, let me tell you some important things about this regular habit of mathematicians.
Think of it in this way – first, we learned to count. So, what was our need to take fractions into account? Maybe, you’ll say we need to measure half a litre of water. OK, but why irrational numbers then? Can you give me any practical daily use of irrational numbers? If you’re bursting to say that we need π to deal with circles, then give it a deeper thought- in our regular life, do we really need π or do we need 22/7 ? I hope, I could make my point.
It seems like it’s a humane tendency to look for what happens when we proceed to work with a more generalized case. Who knows, maybe we hope for getting one general theory for everything…
Now back to our point. Here comes the final blow. Mathematicians were quite upset since ζ((a, b)) only made sense when a > 1. So, they decided to generalize the function over all (a, b). That essentially means that we need to define a value at those points where the function is not making sense. Now, if we are to put just any value, we can do anything we want. well, yes, but no.
Here come into play something called Analytic Continuation, which I better not try to go deep into. But what it basically does, is to give you one and exactly one particular way to continue a function to areas in which it is undefined. When you apply the analytic continuation to the Riemann Zeta function, it turns out that you have forcefully assigned the value –1/12 to the point x = −1. In other words, you forced ζ(−1) = –1/12 .
If you’re still not jumping with excitement, put x = −1 into ζ(x) and see what happens. Since, 1/n-1 is simply n,
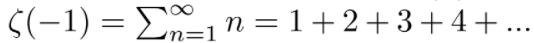
which is, –1/12 .
So, now you understand what my professor meant by defining addition in a different way.
In case, you are a little confused about the analytic continuation part (which is quite natural given the mathematical abstractness of the concept), here’s a little more elaboration on that part
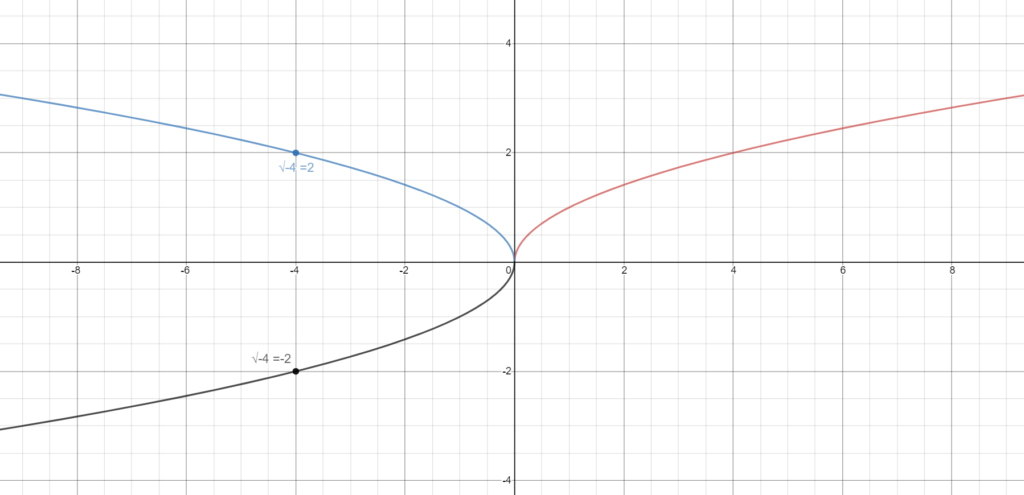
Think of the function f(x) = √x . Of course, this function makes sense only for non-negative values of x. But, for a moment think that you are a mathematician and you want to generalize this function for the negative part as well. One very natural way to do so is to simply mimic the positive part on the other side (i.e., reflect the positive part through the Y-axis). Your friend may try a second approach to generalize it- he/she may find it natural to take the reflection of
√x through the origin. Now, according to your generalization, √−4 = 2, and according to your friend’s generalization, √−4 = −2.
Now, none of these results is correct according to the strict mathematical sense. But, they make perfect sense once the corresponding generalizations are taken into account. Now it turns out that analytic continuation is simply one such way to generalize the zeta function (and for some reasons, mathematicians find this generalization more natural than anything else). And corresponding to that generalization, ζ(−1) = –1/12 .
A Chance To Win $1,000,000
As promised, here’s your chance to win $1,000,000. You only need to wort out another fun exercise.
Just like our analytic continuation forced −1/12 on the point x = −1, it has also forced 0 on all negative even integers. These are called the trivial zeros of the function. We also know that any other point where the function is 0 must be of the form (a, b) where 0 < a < 1. Now, Riemann hypothesized that these points must have a =1/2.
So, here’s what you need to do to win that sum of money. You either need to prove the hypothesis, or you need to find a point (a, b) where 0 < a < 1 but a ≠ 1/2.
What’re you waiting for? Go on and give it a try.
Conclusion
Next time you say all natural numbers sum up to −1/12 , you better know what you mean.
Or do this. Take a vow that you’ll say such a thing only after you’ve proved the Riemann Hypothesis.
Written by Sayan Dutta (2nd-year BS-MS, IISER Kolkata)
Extras:
If you want to know more about this topic, here are a few cool YouTube videos that I would recommend:
- Visualizing the Riemann zeta function and analytic continuation (highly recommended)
- Numberphile v. Math: the truth about 1+2+3+…=-1/12
- Ramanujan: Making sense of 1+2+3+… = -1/12 and Co.
- Riemann Zeta Function
About the Author:

I am Sayan Dutta studying in IISER Kolkata with a major in mathematics. Apart from my academic interests, I am also an ardent reader, a film buff, and have keen interests in using the pen as a medium of communication (well, not really the pen; the keyboard to be more literal).
This is Sayan’s first blog for TQR!